Table of Contents
- Linear regression using Pytorch
- Linear regression model in Pytorch
- Fine-tuning Linear Model
- Testing Performance of the Model
1. Linear regression using Pytorch
- To implement the neural network that acts as a linear regression model. First we will create our own data set. Will take one value of x and we should get a corresponding value of y from a simple linear equation and we will fit a linear regression model that will try to predict that equation.
- To create our own dataset, we have import numpy and to plot our data points we import matplotlib.pyplot.
- Lets take first 10 positive integers, from 1 to 10 and we are inserting those values in x and we are getting the corresponding value of y from the equation as shown in the figure 1 which is a linear equation.

Figure 1: creating the datasets
We are creating a list from 1 to 10 naming it as x_values as you can see figure 2. From that we are creating numpy array from that list and we calling it as x_train. From that will be doing some pre-processing on the data. Once we create numpy array from the list, numpy array will look like as shown in figure 2.
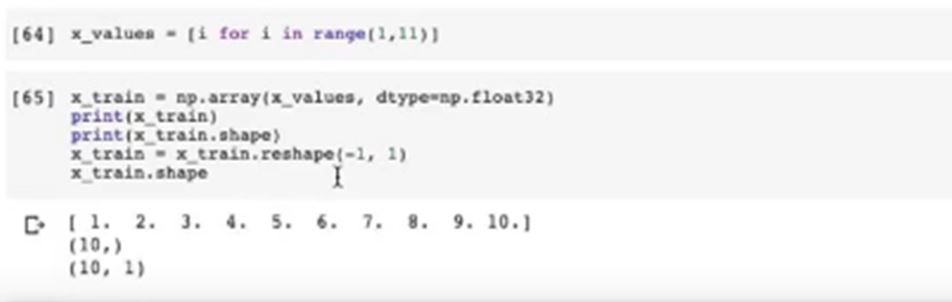
Figure 2: creating the values
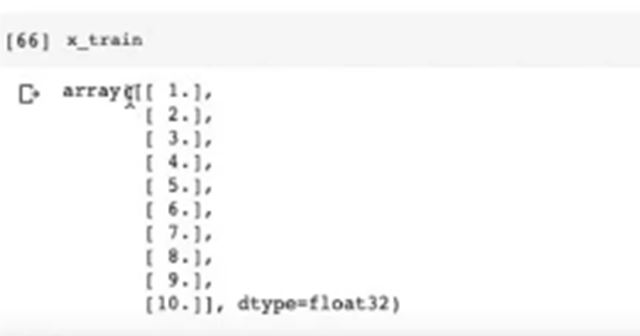
As you can see in figure 2, the open-ended array is a problematic thing in Pytorch, as Pytorch can’t work on this so we reshape the array as you can see in figure 3. As you can it is an array of small arrays as it contains small element 1to 10.
As we plot the data, we can see in figure 4, it will form a straight line, because it comes from the linear equation of y as you can see in figure 1.

2. Linear regression model in Pytorch
Here we will build a linear regression model in Pytorch that will try to credit the equation mentioned above.
- First we will import torch.
- Then from torch.autograd we will import variable.
- Then we will import torch.nn as nn because that has all the modules for implementing deep neural networks.
- For optimization we are importing SGD from torch.optim.
- Then we will create a linear regression model class, we have named it as LinearRegressionModel.
- Call the init function
- Then define a super()which will call itself.
- Since we have only one dimension for the input variable and one dimension for the output variable we are calling nn.Linear(1 , 1) as shown in figure 5.

- Then we are declaring our forward path basically calling the linear on the x value.
- Once we have created our Linear model regression class we will instantiate it under Linear_model.
- Then we will call CUDA as shown in figure 6 so that we can use the GPU from the model. Then you can check the parameters.

3. Fine-tuning Linear Model
- To fine-tuning our linear model we have two aspects, which are loss function and optimizer. As we have discussed before, that loss functions can take many forms.
- In this linear regression model, we are using nn.MSELoss, that means Mean Square Error for optimization we are using Stochastic Gradient Descent (SDG) as you can see in figure 7.

- Choose the number of epoch wisely, here I have chosen 1000 as you can see in figure 8, we think ideally that will be perfect.
- Then we calling the input variables, and then we creating labels as it initializes all the gradients of each epoch
- Then output values have all the predicted values, that the input value predicts. Then you can calculate the loss and you can see in figure 8, it is done through MSE and it compares the output that is the predicted variables. Then output actual labels is from the equation.
- After that, we call Loss.backward() and then we call optimizer.step basically it calls the optimizer.

Once we run it, we can see that, the loss started from 524.12 as you can see in figure 4 and gradually it decreased and the last step, that is on thousand epoch, it give 0.0081 in figure 9.

- If you loss of each epoch is decreasing, your model is learning, that means it is on the right track.
- After that we plot our predicted our true values, which is shown in figure 4, the predicted value will come on blue lines and the true values are the red dots.
Now lets check our loss in decreasing at each epoch. As you can see in figure 10 our loss value is getting decreased which is a sharp down.
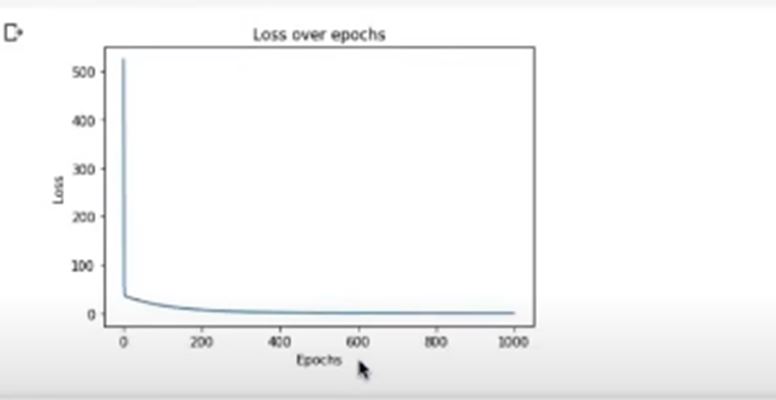
4. Testing Performance of the Model
Now lets verify that our model is working or not. To test the performance of the model we take three values which are 100. 200 and 300 as you can see in figure 11. Then you can check the real values by adding these values of the array. Then we will check how our model predicts the value As you can see the figure 11. As you can see the predicts values and pretty close to the real values.
